Introduction
Sin 60 Degree: Imagine you have a right triangle. Which is just a rectangle with one angle at 90 degrees, like a square triangle. Now, we are interested in one particular angle of this triangle, let’s say 60 degrees. This is where trigonometry comes into play. We use three basic functions for this: sine, cosine, and tangent. commonly abbreviated as sin, cos, and tan.
About: Sin 60
For our 60-degree angle. The sine (sin) of that angle helps us find the length ratio of the opposite side. The length of the hypotenuse is an angle (the longest part of a triangle, as opposed to a right angle). So in summary, if you know the angle is 60 degrees. If you want to find the ratio of the longest side to the opposite side, you use the sine function. It’s like a tool that helps solve puzzles involving triangles. So imagine a triangle with one corner at right angles, meaning 90 degrees. That looks like the corner of the triangle. Now consider the other two aspects. Adding degrees to those angles equals the third angle. So, if one angle is 90 degrees, the other two add up to 90 degrees.
Now, there are different angles that we care about 0, 30, 45, 60, and 90 degrees. This makes it easier to solve our square puzzles. Let’s talk about the sign. The sine (sin) is like a helpful tool that tells us about a particular angle in our triangle. Let’s say that ∅ for any angle, sin ∅ is just a fancy way of saying “perpendicular divided by Hypotenuse”. The vertical is the vertical section straight up. The hypotenuse was the longest segment. So, if you know the angle ∅, and you want to know about the angles
Sin 60: degrees and radians
So in trigonometry, we use something called degrees to measure angles. It’s like the language of squares and squares.
Imagine a watch, the whole thing is 360 degrees. Every quarter hour looks like a slice, and that’s 90 degrees.
Now, degrees can be broken down into even smaller units – like minutes and seconds. Those are the little details when you want to be super precise.
However, there is another way to talk about angles, and that uses something called radians. It looks like a different way of measuring an angle, and for that, we use a different symbol, π (pi). π is like 180 degrees.
Think of a unit circle like a superhero circle with one radius. The total circle is 2π radians. Another way to color parts, as if using a special superhero costume!
Values of angles and radii
Thus, there are three basic axes when dealing with angles: sin (sine), cos (cosine), and tan (tangent). We can find their values for angles from 0 to 90 degrees.
Then tan (∅), which is the tangent, is like the sum of sin (∅) and cos (∅). It’s like, “Hey Tan, what’s your deal?” And Tan goes, “I just broke up with Pap Kos!”
But here’s the cool part – we don’t have to memorize all the values for every angle. We just focus on the basics and essentials, especially from 0 to 90 degrees. Once we know them, we can use some techniques to determine the value of the other aspects. It’s like learning the basic moves of the game before mastering all the advanced moves. (Sin 60 )
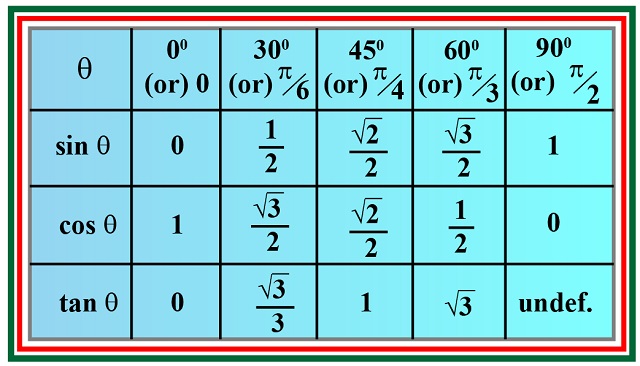
Some values of Sin, cos, tan
- sin 30° = ½
- Sin 45°= 1/√2
- Sin 60°= √3/2
- Without 90°=
- Cosine:
- Cos 0° = negative 90° =
- Cos 30°= Sin 60° = √3/2
- Cos 45° = Evil 45° = 1/√2
- Cos 60° = Sin 30° =½
- Cos 90° = sin 0° = 0
Tangents:
- Tan 0° = Sin 0°/Cos 0° = 0
- Tan 30° =1/√3
- Tan 45° = 1
- Tan 60° = √3
- Tan 90° = ∞
Conclusion
In this blog, we come to know various things about the trigonometry. By using certain terms such as angles, degrees, and radiants. And also we unlocked the secret of the right-angle triangles. In this journey through triangles, angles, and functions. And we’ve gained the tools to navigate and solve puzzles. Hence, trigonometry is not just a mathematical concept. but a practical and powerful tool for understanding the relationships within triangles.( Sin 60 )


