Quadratic equations are the basis of algebra. Hence it plays an important role in mathematics and practical applications. In this equation, x2-11x+28=0 stands out and is popular. Originally considered a complex mathematical puzzle. When approached with the right tools and logic. It turns into a fascinating journey through the complex terrain of quadratic equations
Understanding Quadratic Equations:x2-11x+28=0
The general form of the quadratic equation is ax2 + bx + c = 0, where a, b, and c are constants. In our equation x2-11x+28=0, a = 1, b = -11, and c = 28. The solution to this equation is to find a satisfying value of x.
Factorizing a quadratic equation:x2-11x+28=0
One of the basic methods of solving quadratic equations is multiplication. In this case, we aim to express the equation as a product of two binomials. For x2-11x+28=0, binomial factors can be found whose product is equal to the product of a and c (ac) and whose sum is equal to b
In our equation, a = 1, b = -11, and c = 28. The result is ac 1 28 = 28. We are looking for two numbers that multiply 28 and add to -11. Those numbers are -4 and -7 because (-4) (-7) = 28, and (-4) + (-7) = -1
Thus, we can express the quadratic equation as (x – 4)(x – 7) =
If you set any factor to zero:
Now that we have factored the quadratic equation, we can solve for x by setting each factor to zero.
(x – 4) = 0 → x =4
(x – 7) = 0 → x =7
Thus the solutions of the quadratic equation x2-11x+28=0 are x = 4 and x =7
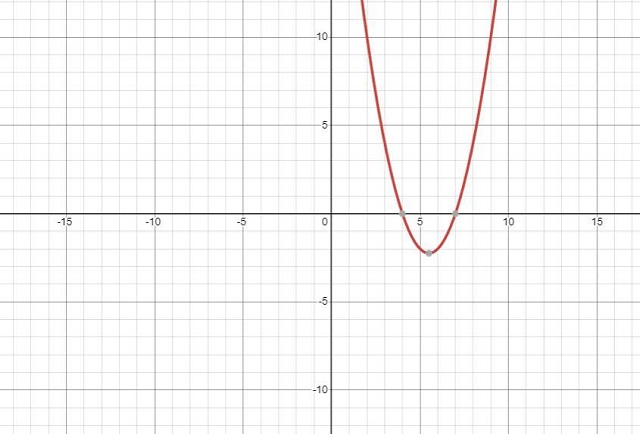
To visualize the solution, we can plot the quadratic equation. The graph of y = x2-11x+28 is an open parabola above. By finding the x-intercepts (where y = 0), we place the points (4, 0) and (7, 0) on the graph representing the solution obtained algebraically
Real-world applications:
Quadratic equations are not just abstract mathematical concepts. They have practical applications in various industries. A common application is physics. Where these equations describe the motion of a rocket. Engineers use quadratic equations to optimize systems and solve complex design problems.
Challenges and changes:
Although the quadratic equation x2-11x+28=0 is well solved. Hence, it is important to realize that not all quadratic equations are easily factorable. Some may require other methods such as using quadratic formulas. Or square completions use the appropriate
Quadratic Theory.(x2-11x+28=0)
The quadratic formula is a powerful tool. That provides an easy way to find the solution of any quadratic equation. For the quadratic equation ax2 + bx + c = 0, the solution (root) can be determined by the following formula.
x2−11x+28=0
Use the quadratic formula to find the solutions.
−b±√b2−4(ac)\2a
Substitute the values a=11, b=−11, and c=28 into the quadratic formula and solve for x.
11±√(−11)2−4⋅(1⋅28)2⋅111±(-11)2-4⋅(1⋅28)2⋅1
Simplify.
x=11±32The final answer is the combination of both solutions.
x=7,4
Ending the class is like providing a modification to simplify solving a quadratic equation. It is slightly more complicated than other methods. However, it is easy to solve complex quadratic equations.
Now, let’s talk about x2-11x+28=0. We looked for ways to solve it, like factoring, graphing, and using the quadratic formula. Each method gives us a different perspective on how to break the law of quadratic equations. These statistical tools are not just abstract concepts. They are super useful in real-life fields like physics and engineering. So let’s discuss these quadratic equation mysteries and get a glimpse into the cool and connected world of mathematics.
Final words
Finally, the idea of x2-11x+28=0 seemed like a cool trip down the solution path. We tried things like factoring and graphing using the quadratic formula. Each method taught us a different way to solve quadratic equations. These accounting tips aren’t just fancy accounting ideas. They are super useful in real-life stuff like physics and engineering. So by solving the mystery of quadratic equations. Hence, we learned a lot about how math works and fits together beautifully.


